東大数学対策
数学は、東大入試1日目の午後に行われる試験科目です。
文科各類（文系）は100分で4題（80点満点）、理科各類（理系）は150分で6題（120点満点）の記述式の問題を解くことになります。
東大数学の試験概要
出題形式
例年、文系は大問4問、理系は大問6問の問題が出題されます。全問記述式です。
出題範囲
文系は数学Ⅰ・数学A・数学Ⅱ・数学Bから出題されます（数学Bは数列・ベクトルから出題）。
理系はこれらに加え数学Ⅲの範囲からも出題されます。
試験時間・配点
数学の試験は、東大二次試験の2番目の科目であり、1日目の午後に実施されます。
| 文理 | 試験時間 | 配点 |
|---|---|---|
| 文科各類（文系） | 1日目 14:00～15:40（100分） | 80点 |
| 理科各類（理系） | 1日目 14:00～16:30（150分） | 120点 |
配点の内訳
東大数学の配点は、文系80点、理系120点ですが、その内訳（大問ごとの配点）は非公開です。
大方の予想では、各大問20点配点で、文系は20点×4の80点満点、理系は20点×6の120点満点とされています。
（理系の第3問・第6問は、解答欄が大きいこともあり、配点が他の問題よりも少し大きいのではとする説もあります。）
解答用紙
A3両面です。
文系は解答用紙1枚で、表に第1問・第2問、裏に第3問・第4問の解答欄という形式です。
理系は解答用紙2枚で、1枚目表に第1問・第2問、裏に第3問、2枚目表に第4問・第5問、裏に第6問の解答欄という形式です。
解答欄は無地で、ノートのような罫線は入っていません。
解答欄にそのまま解答を記述していってもいいですが、解答欄が不足する恐れがあるので、まず解答欄の真ん中に縦線を引き、解答欄を左右に二分割して解答を記述していく手法をおすすめします。
東大数学の基本戦略
目標点
文系
合格者平均点は37点ほど（2021年度入試）ですので、80点満点の半分の40点（1完2半ぐらい）超えが分かりやすい目標になるでしょう。科類による差はあまりありません。
理系
合格者平均点は、理一が67点ほど、理二が54点ほど、理三が86点ほど（2021年度入試）でした。
理一と理二で合格最低点が大きく異なる主因は、この数学にあると思われます。実に13点も差がついています。（採点基準が大きく違う様子は見受けられないので、数学が比較的得意な受験生が理一には多いものと推測されます。）
さて、目標点ですが、合格者平均点よりやや上を見て、理一は70点（2完3半、3完1半ぐらい）、理二は60点（1完4半、2完2半ぐらい）、理三は90点（3完3半、4完1半ぐらい）を目標としましょう。
部分点を狙う
東大数学の採点は答えに至るロジックを重視するため、たとえその問題を完答できなくても、部分点狙いで、解答方針や思考のプロセスはできるだけ書くようにしましょう。
東大数学（文系）おすすめ参考書・問題集
本サイトで紹介する勉強法・参考書は一例です。ご自身の現在の学力や学校・塾の授業進度等に応じて、適宜調整ください。
1冊の参考書・問題集は、7～8割方解けるようになったら、上のレベルの参考書に進んでも構いません。ただし、上のレベルの参考書が全く手につかないようであれば元の参考書に戻る（もしその参考書はやり尽くしたということであれば、元のレベル帯の別の参考書を使用する）、という勉強法が基本です。数学は基礎が大切です。一歩一歩着実に進んでいきましょう。
基礎レベル（基礎のインプット）
チャート式 基礎からの数学Ⅰ+A
チャート式 基礎からの数学Ⅱ+Bまずは、青チャートなど、学校で配られたであろう基礎的な問題集の例題を一冊仕上げましょう。
1対1対応の演習/数学1 新訂版 (大学への数学 1対1シリーズ)
1対1対応の演習/数学A 新訂版 (大学への数学 1対1シリーズ)
1対1対応の演習/数学2 新訂版 (大学への数学 1対1シリーズ)
1対1対応の演習/数学B 新訂版 (大学への数学 1対1シリーズ)入試の典型題の解法を学ぶ参考書。チャート式と併用するのがおすすめ。
基礎演習レベル（アウトプットの練習）
新数学スタンダード演習（大学への数学 4月増刊号）毎年4月に出ている大学への数学の増刊号です。数学Ⅰ・A・Ⅱ・Bが対象で、青チャート等の基礎的なレベルの問題集が理解できていれば解けるぐらいの難易度になっています。もし全く解けないようであれば、演習不足のため、青チャート等をもう一度見返しましょう。
文系数学の良問プラチカ 数学1・A・2・Bやや難しいですが、良問揃いです。なお、なぜか『文系プラチカ』は『理系プラチカ』より全体的に難しい構成になっています。なぜなのか。
応用レベル（過去問演習）
この段階で東大過去問演習に進んでしまってよいでしょう。ただ、もしも全く手につかないということであれば、前のレベルに戻って、もう一度参考書・問題集を解き直したいところです。
東大数学で1点でも多く取る方法 文系編[第4版]分野別に、2004～2018年度の問題を整理した、東大入試数学の過去問集です。
格好いい解法ではなく、部分点を稼ぎやすい解法や、類似問題に出会ったときに同じように解ける解法など、地道で確実な解法に主眼を置いた参考書となっており、おすすめです。
鉄緑会 東大数学問題集 資料・問題篇/解答篇 1981-2020〔40年分〕他の過去問題集を圧倒する内容量
と値段の参考書。鉄緑会マニアにはたまらない一品です。実戦的なアドバイスや別解が豊富で良質な過去問解説書であり、自己採点用の採点基準もついています。
40年分もいらない、直近10年分で十分だという方は、毎年7月に出版される『鉄緑会東大数学問題集 資料・問題篇/解答篇』をどうぞ。
東大・入試数学50年の軌跡【1971年~2020年】 (大学への数学)50年分の東大入試数学をまとめた過去問集。月刊「大学への数学」入試特集号および増刊号「入試の軌跡/東大」の記事に加筆修正を加えた問題集（参考書）です。
50年分もいらない、直近10年分で十分だという方は、毎年6月に出版される『入試の軌跡/東大（大学への数学 6月増刊号』をどうぞ。
東大数学（理系）おすすめ参考書・問題集
本サイトで紹介する勉強法・参考書は一例です。ご自身の現在の学力や学校・塾の授業進度等に応じて、適宜調整ください。
1冊の参考書・問題集は、7～8割方解けるようになったら、上のレベルの参考書に進んでも構いません。ただし、上のレベルの参考書が全く手につかないようであれば元の参考書に戻る（もしその参考書はやり尽くしたということであれば、元のレベル帯の別の参考書を使用する）、という勉強法が基本です。数学は基礎が大切です。一歩一歩着実に進んでいきましょう。
基礎レベル（基礎のインプット）
まずは、青チャートなど、学校で配られたであろう基礎的な問題集の例題を一冊仕上げましょう。
チャート式 基礎からの数学Ⅰ+A
チャート式 基礎からの数学Ⅱ+B
チャート式 基礎からの数学Ⅲ
入試の典型題の解法を学ぶ参考書です。チャート式と併用するのがおすすめです。
1対1対応の演習/数学1 新訂版 (大学への数学 1対1シリーズ)
1対1対応の演習/数学A 新訂版 (大学への数学 1対1シリーズ)
1対1対応の演習/数学2 新訂版 (大学への数学 1対1シリーズ)
1対1対応の演習/数学B 新訂版 (大学への数学 1対1シリーズ)
1対1対応の演習/数学3 微積分編 (大学への数学 1対1シリーズ)
1対1対応の演習/数学3 曲線・複素数編 (大学への数学 1対1シリーズ)
基礎演習レベル（アウトプットの練習）
新数学スタンダード演習（大学への数学 4月増刊号）毎年4月に出ている大学への数学の増刊号です。数学Ⅰ・A・Ⅱ・Bが対象で、青チャート等の基礎的なレベルの問題集が理解できていれば解けるぐらいの難易度になっています。もし全く解けないようであれば、演習不足のため、青チャート等をもう一度見返しましょう。
数学Ⅲスタンダード演習（大学への数学 5月増刊号）『新数学スタンダード演習』の数学Ⅲ版です。こちらは毎年5月に大学への数学の増刊号として出版されています。
こちらも、もし全く解けないようであれば、青チャート等をもう一度見返しましょう。
やさしい理系数学 三訂版「やさしくない」ことで有名な、通称『やさ理』と呼ばれる演習書です。
典型解法が身についている受験生用です。
文系数学の良問プラチカ 数学1・A・2・B
理系数学の良問プラチカ 数学3東大志望であれば、数学1A2B対策のプラチカは（なぜか理系プラチカより難しい）文系プラチカをおすすめします。
応用レベル（過去問演習）
この段階で東大過去問演習に進んでしまってよいでしょう。ただ、もしも全く手につかないということであれば、前のレベルに戻って、もう一度参考書・問題集を解き直したいところです。
東大数学で1点でも多く取る方法 理系編[第4版]分野別に、2004～2018年度の問題を整理した、東大入試数学の過去問集です（行列・1次変換を除く。複素数平面は2000年度以降）。
格好いい解法ではなく、部分点を稼ぎやすい解法や、類似問題に出会ったときに同じように解ける解法など、地道で確実な解法に主眼を置いた参考書となっており、おすすめです。
鉄緑会 東大数学問題集 資料・問題篇/解答篇 1981-2020〔40年分〕他の過去問題集を圧倒する内容量
と値段の参考書。鉄緑会マニアにはたまらない一品です。実戦的なアドバイスや別解が豊富で良質な過去問解説書であり、自己採点用の採点基準もついています。
40年分もいらない、直近10年分で十分だという方は、毎年7月に出版される『鉄緑会東大数学問題集 資料・問題篇/解答篇』をどうぞ。
東大・入試数学50年の軌跡【1971年~2020年】 (大学への数学)50年分の東大入試数学をまとめた過去問集。月刊「大学への数学」入試特集号および増刊号「入試の軌跡/東大」の記事に加筆修正を加えた問題集（参考書）です。
50年分もいらない、直近10年分で十分だという方は、毎年6月に出版される『入試の軌跡/東大（大学への数学 6月増刊号』をどうぞ。
発展レベル（高得点取りたい人・理三志望者用）
理系数学で90点以上を目指したい方、もしくは理三志望の方は、過去問演習に加えてもう少し演習をしましょう。
新数学演習（大学への数学 9 or 10月増刊号）毎年9月か10月に出ている大学への数学の増刊号です。
東大理系数学の過去問が初見で70点ぐらいは取れる受験生で、さらに上を目指して90点以上取っていきたい方向けの参考書（問題集）です。基礎・応用がしっかりしていない状態で本参考書を使用するのは効果が薄いのでご注意ください。
テーマ別演習① 入試数学の掌握 総論編
テーマ別演習② 入試数学の掌握 各論錬磨編
テーマ別演習③ 入試数学の掌握 各論実戦編東大・京大・阪大の入試数学問題を中心に、難問を体系立てたアプローチで解説した参考書（問題集）です。3桁の大台に乗せて数学を絶対的な得点源にするんだ、という方向けです。
新課程入試対応 数学難問集 100通称『黒チャート』。数学マニア用。何もかもやり尽くして、暇で暇でしょうがない人向けです。
東大数学のQ&Aまとめ
数学はセンスなのか
理47-858：大学への名無しさん：2010/03/14(日) 23:57:55 DgZ3q/t40
数学はセンスだろ
理47-859：大学への名無しさん：2010/03/15(月) 00:00:01 ipP3CHGI0
センスで解ければ言うことないけど
センスが無くても地道な方法で点数は取れる
理47-860：大学への名無しさん：2010/03/15(月) 00:01:10 pzKt2Ou20
典型問題の解法覚えるに尽きる
理47-861：大学への名無しさん：2010/03/15(月) 00:25:48 p7sRaErI0
現役時模試で80台でも本試で20しか来なくて落ちた俺ガイル
結局何が悪かったんだろうな
理47-863：大学への名無しさん：2010/03/15(月) 00:27:59 Mir1wkqX0
解法の習得範囲に穴があってそこばっかり突かれたんだよ
要するに勉強不足
理47-866：大学への名無しさん：2010/03/15(月) 01:01:49 MAlOBCF60
東大数学は典型問題や有名問題の解法覚えるだけではどうにもならない
理47-867：大学への名無しさん：2010/03/15(月) 01:04:02 yJTnjUjKP
>>866
そういう問題はどうせ誰も出来てないから差がつかない
理47-868：大学への名無しさん：2010/03/15(月) 01:06:44 /zxQZBwh0
数学が苦手レベルなら解けなくても大丈夫。
他ができないなら救いようがない。
理47-869：大学への名無しさん：2010/03/15(月) 01:16:29 WnQ1eVKU0
ここ最近の傾向なのかは分からんが
模試の時は数学の高得点に引っ張られて良い判定が出たものの
本番では数学が想定していたほど取れずに撃沈、って人が多い気がするな
他の科目が本番で模試より点が取れるのに比べて数学だけは本番で点数が下がりやすいから
数学のおかげで良い判定を取った人は注意したほうがいい
理47-870：大学への名無しさん：2010/03/15(月) 01:20:01 633cqZ8X0
現役時は２９点足りなかったが、１浪して理一受かった。
浪人初期のテストで、「あれ、俺落ちたけど直前期めっちゃ伸びてたんじゃね！？」
と感じるくらいの成績が取れれば合格フラグ。
理47-873：大学への名無しさん：2010/03/15(月) 02:33:02 CyQSTIka0
>>866
それは違う。
東大の問題は巧妙に受験テクニックが組み込まれたパズル。
ただ、解法のレベルが高い。
理47-881：大学への名無しさん：2010/03/15(月) 11:26:22 yf5iILWV0
現役なら数学はセンスによるところが正直言って大きい
浪人する人で本気で数学を得点源にしたい人がいるなら勉強方法を徹底して突き詰めろ
単なるパターンの暗記、問題演習だけでは全く歯が立たない
いろんな予備校の講師に話をどんどん聞いて普段勉強するときの問題に対する取り組み方とか
解法の糸口をつかむための考え方、テクニックについて質問しまくるといい
理47-882：大学への名無しさん：2010/03/15(月) 11:38:18 W1lTU0EB0
数学が伸びる奴ってのはもともとセンスがあるんだよ。
周囲見てると間違いなくそう。数学が得点源になるほどできる奴ってのはもともとセンスがある。
だからある程度勉強しても東大数学であまり得点できない奴は数学を見切って、理科や英語、古典に
集中したほうがいい。ハッキリ言ってこれらの科目は誰でも伸びるから。
数学にハマって他の科目に手が回らなくなるのが一番ヤバいよ。
もちろん理Ⅲだと数学ができないとどうしようもないけど。
理47-883：大学への名無しさん：2010/03/15(月) 11:49:02 MAlOBCF60
たとえば1対1やるにしても青チャやるにしても、書かれている解法の理解と記憶だけで満足して
別解の探求とか問題の条件変えることによって解法がどう変化していくかとか、そういうことに
普段から無頓着な人間はどんな参考書使っても大して伸びない
理47-884：大学への名無しさん：2010/03/15(月) 11:50:14 W1lTU0EB0
ただ英語も量は膨大だからこれまでサボっていた人は、勉強すれば徐々にだが確実に学力は
伸びるとはいえ、かなり苦労すると思う。
鉄力の見解によれば東大受験に一般的に必要な勉強量の比は
数学10 英語10 国語3 理科5
理47-891：大学への名無しさん：2010/03/15(月) 12:58:10 yWcKy+2o0
ってかセンスって何ですか？
理47-893：大学への名無しさん：2010/03/15(月) 13:14:27 MvCzNz4b0
>>891
経験上センス云々言う人はそのほとんどが数学が出来ない(というより嫌いな)人で、
それを出来ないことの言い訳にしてるんだよね。
それ以前の圧倒的な量の差を見過ごしてると思われる。
確かに数学に対する嗜好や興味の差というものはあるかもしれないが、
先天的な能力による優劣はほとんど無いと言っていいと思う。
理47-894：大学への名無しさん：2010/03/15(月) 13:32:34 MvCzNz4b0
でも中には自分が他人よりセンスがあるから自分は出来るんだ
と考えてる自意識過剰な人間も少なからずはいる。
自分も昔はそうだったが、数学をより深く学び、
レベルの高い人間と出会うにつれてそんな感覚は薄れていったね。
数学が出来るようになりたいならまず数学を好きになること。
まぁそれがなかなか簡単なことではないんだけどね。
ただこれだけはいえるかな。
数学が出来る人(東大受験生も一目置くレベル)で、
数学を単なる受験科目の１つと考えてる人はおそらくいない。
何かしら興味や嗜好といったものを持ってる。
理47-904：大学への名無しさん：2010/03/15(月) 18:40:35 pzKt2Ou20
センスが必要だとか単純な暗記じゃ歯が立たないとかいうのは数学8割とか取るレベルの話だろ
理ⅠⅡなら問題ない
大学で習う数学公式は使ってよいか
大学入試の数学において、高校では習っていない公式等を使用することについては、以下の理由から使用しても問題はないものと思われます。
- 大学を受験するのは何も高校生や浪人生だけではない。一度大学を卒業した方や社会人の受験生もいる。そのような方々に高校数学のみを用いた解答は強制できない。また、答案に個人情報は載らないので、答案の区別もできない。
- 東大の募集要項や出題の意図、数学の問題用紙等に、高校数学のみを用いて解答せよとの記載はない。
- 大学の教科書を読んで勉強している意欲的な高校生の学習を、大学側が制限する道理はない。
ただし、公式等をきちんと理解していないままに使用すると、論理不十分で減点される可能性があります。特殊な条件で成立する裏技的な公式の場合、公式に前提条件がくっついているはずです。この前提条件を示して公式を使用しないと、そもそも公式が成立するか分からない条件下で勝手に公式を使用していることになるので、減点されてしまうと思われます。
理24-379：大学への名無しさん：2009/02/24(火) 06:43:36 U0Rosskj0
今更だが、バウムクーヘン分割（求積）って当然のように使っていいよな？
教科書に載ってたっけ？
東大は論理的な誤りが無いならば、大学の知識でも証明すら不要でバンバン使っていいというのが常識だけど、バウムは高校の内容だよな。
ヤバイのはパップスギュルダンくらいだろ？
理24-380：大学への名無しさん：2009/02/24(火) 06:53:33 Z0SPOblnO
いいんじゃね？
てか俺早稲田で面積求めるとき普通に外積使っちゃったしな……
個人的にはそっちの方が心配
理24-382：大学への名無しさん：2009/02/24(火) 07:02:40 WXanmtOzO
いくらつかっていいっていっても不安なんだろ
つかわなきゃいいよ
理24-384：大学への名無しさん：2009/02/24(火) 07:21:04 U0Rosskj0
>>382
いや、バウムに関しては全く不安は無い。
ただ、なんどかネタか煽りか知らんが、バウムは使うとダメみたいな変なレスを見たきがするので聞いただけ。
パップスは使わん。超特殊な条件でしか使い物にならんからな。（大数軌跡）
理24-385：大学への名無しさん：2009/02/24(火) 07:25:13 5N7k6k11O
やっぱり合同式つかっちゃ駄目なのか
理24-386：大学への名無しさん：2009/02/24(火) 07:41:53 SnuwSY4IO
使えそうならヤコビアンでもパップスギュルダンでも使ってやるぜ
理24-387：大学への名無しさん：2009/02/24(火) 07:46:21 wXQapxqVO
バウムは近似式を示せば使っていいと言われたが…
合同式はどうなんだろ
理24-388：大学への名無しさん：2009/02/24(火) 07:47:56 nMcHkDw7O
まだ大学に行ってないのに大学の知識かどうかなんて分からん。
バウムなんて数行の式変形で導けるし、
リスクを背負ってまでその数行を省略しようと思わない。
理24-396：大学への名無しさん：2009/02/24(火) 08:23:30 lwkNNt81O
合同式や互除法は使って良いだろ。
むしろバームの方が不安なんだが。
理24-398：大学への名無しさん：2009/02/24(火) 08:54:44 eeW2wQtX0
バームクーヘンは減点される可能性高いと思う
ソースは88年の問題。置換がわかってる人は置換で
理24-402：大学への名無しさん：2009/02/24(火) 09:21:39 6Qtzs24gO
俺はロピタル使うぜ
理24-404：大学への名無しさん：2009/02/24(火) 09:26:52 w0yk5nAC0
>>398
お前は加法定理使ったら減点だというの？
理24-405：大学への名無しさん：2009/02/24(火) 09:26:59 U0Rosskj0
それじゃ、バウムは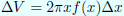
と表せるから～ とか１行と簡単な図をいれるだけでＯＫ？
理24-407：大学への名無しさん：2009/02/24(火) 09:29:29 l3rDUCT/O
本質的に東大が何を聞きたいか考えれば何を使っていいか,いけないのかはわかるはず
理24-408：大学への名無しさん：2009/02/24(火) 09:29:46 EPG3t35+0
文部省指定の教科書に載ってる公式は使っていいってのが基本
まあ俺は減点覚悟で使うけど
理24-614：大学への名無しさん：2009/02/24(火) 18:53:49 UJN7ZlYq0
大数に書いてあった注意点![lim[n→∞] f(n)](m/lim.png)
の値を出す時![lim[n→∞] logf(n)](m/lim_log.png)
の値を経由するとき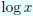
のグラフの連続性に触れていなきゃ減点、らしい
理24-616：大学への名無しさん：2009/02/24(火) 18:57:15 h00rt8brO
>>614
それは有名だよな
東北大でも対数連続性ふれてないの減点する
って教授が言ってた
模試等の解き直し
模試等の試験問題の解き直しは、ただ模範解答を読んで済ませるのではなく、実際に手を動かして解き直しを行いましょう。分かってるつもりでも途中の論理で詰まったり、何気ない式変形で詰まったりして、思わぬ弱点が分かることもあります。
第1問は簡単？
例年、数学の第1問は文理ともに比較的簡単な問題が配置される年が多いです。
ただし、稀に難しい（解きにくい）地雷問題が配置される年もあります。第1問が解けなかったからといってペースを崩してしまわないようにご注意ください。こんなに難しいなら誰も解けないから大丈夫、と思い込むことにしましょう。
予備校の解答速報は見てもよいか？
入試1日目の夜ぐらいには、予備校や数学マニアの有志が、自身の解答速報をネットやSNSにアップし始めますが、東大受験生の皆様は、入試が終わるまで絶対に解答速報は見ないようにしましょう。まだ2日目の科目もあるのに、ペースが乱れます。気になるその問題は合っていたことにしてください。
同様に、入試が終わるまではTwitter等のSNSも開かないのが無難です。あと1日ぐらいは我慢しましょう。
東大数学の有名問題
加法定理の証明（1999年度第1問（文理共通））
(1) 一般角θに対して sinθ, cosθ の定義を述べよ。
(2) (1)で述べた定義にもとづき，一般角α, βに対して 円周率が3.05より大きいことを証明せよ。
理24-541：大学への名無しさん：2009/02/24(火) 17:42:14 UJN7ZlYq0 理24-580：大学への名無しさん：2009/02/24(火) 18:20:16 UJN7ZlYq0 理24-581：大学への名無しさん：2009/02/24(火) 18:23:13 vgMfWFwe0 順次更新予定です。
sin(α+β) = sinα cosβ + cosα sinβ ,
cos(α+β) = cosα cosβ - sinα sinβ
を証明せよ。
円周率が3.05より大きいことの証明（2003年度第6問（理科））
東大数学ネタ
証明問題に使える裏技！！
じゃあ俺も良問を一つ
「3 以上の自然数 n について、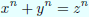
となる 0 でない自然数 (x, y, z) の組み合わせがないことを証明せよ」
まあ東大受験生にとっては標準的な問題かな
これできなきゃ受からないかもね
証明問題がでてきたらそれ使えるな
この命題に関して、私は真に驚くべき証明を見つけたが、
東大の解答用紙はそれを書くには狭すぎる
教授「この程度の命題の証明を発見しただけで驚くとかレベル低いから他の大問からも減点しておこう」
勉強法・参考書まとめページ一覧